BacktotheBasic - 탐색(이진탐색)

이진 탐색

이진 탐색은 정렬된 데이터 집함에서 사용할 수 있는 ‘고속’ 탐색 알고리즘이다.

1. 데이터 집합의 중앙에 있는 요소를 고른다.
2. 중앙 요소의 값과 찾고자 하는 값을 비교 한다.
3. 목표한 값이 중앙요소보다 적으면 왼편에 대해 검색하고, 크면 오른쪽으로 이진 탐색을 수행한다.
4. 찾고자 하는 값을 찾을때 까지 1~3번을 수행한다.

이진 탐색의 성능

이진 탐색은 탐색을 시도할 때 탐색 대상의 범위가 1/2 로 줄어든다. 데이터집합의 크기를 n이라고 하고 탐색 횟수를 x라고 할때

탐색횟수는 X= log_2*n이 된다.

이진탐색트리

이진 탐색트리는 말그대로 이진 탐색을 위한 이진 트리이다.

왜 이진 탐색 트리가 필요한 걸까?. 이진 탐색을 하기위해서는 첫째, 데이터의 처음과 끝을 알아야 하고, 둘때, 순식간에 데이터 집합의 중앙요소를 계산하고 접근 가능해야 한다. 배열의 경우 인덱스를 이용해서 중앙에 있는 요소를 쉽게 계산 및 접근이 가능하지만 데이터 집합이 리스트라고 생각해 보면, head 와 tail을 이용해서 처음과 끝을 알 수 있지만 그 중앙요소를 알수없기 때문에 이진탐색을 위해서는 이진 탐색 트리 구조가 필요하다.

이진 탐색트리의 규칙은 간단하다.

왼쪽 자식 노드는 부모노드보다 작고 오른쪽 자식노드는 부모 노드 보다 커야 한다.
탐색 또한 간단하다.

목표 값이 현재 노드 보다 더 큰경우 오른쪽 하위 트리에 대해서 다시 한번 탐색을 한다.
반대로 더 작은 경우 왼쪽 하위 트리에 대해서 다시 한번 탐색한다.
이렇게 탐색을 반복한다.

삽입은 조금 복잡하다. 우선 새 노드가 삽입 될 곳을 찾아야 한다. 이진 탐색을 통해서 새 노드가 놓일 곳을 찾아내야 한다.

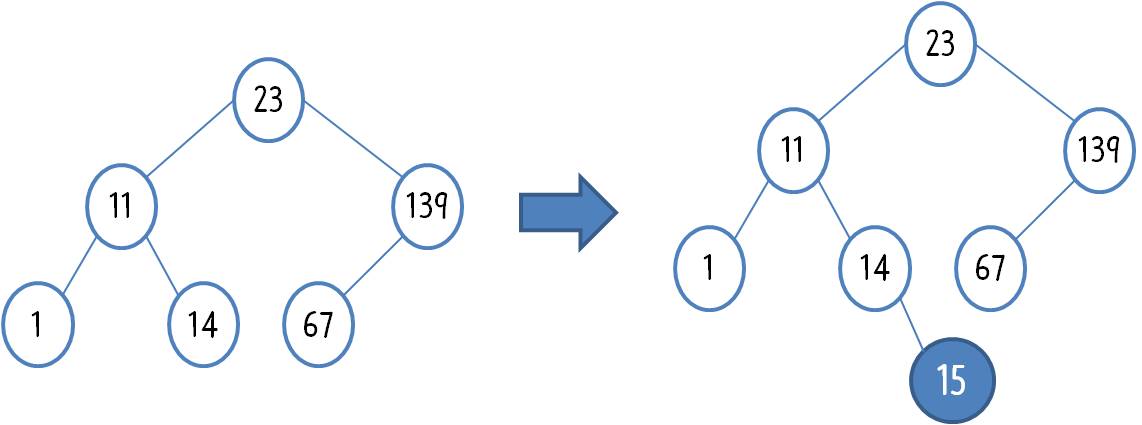
이렇게 생긴 트리데 15를 넣는다면 아래와 같이 진행 될 것이다.
23부터 비교를 한다. 23 보다 15가 더 작다. 23 의 왼쪽 자식 노드가 비어있는지 확인한다. 비어있지 않으므로 왼쪽 트리를 다시 탐색 한다. 11과 15를 비교한다. 11 보다 15가 더 크다. 11의 오른쪽 자식 노드가 비어있는지 확인한다. 비어 있지 않아서 다시 오른쪽 트리를 탐색 한다.
14와 15를 비교한다. 14 보다 15가 더 크다. 14의 오른쪽 자식 노드가 비어있는지 확인하다. 비어있다!! 14의 오른쪽 노드로 15를 넣는다.

이진 탐색 노드의 삭제는 어떻게 될까?
조금 더 복잡한 이진 탐색 트리를 예로 들어 보자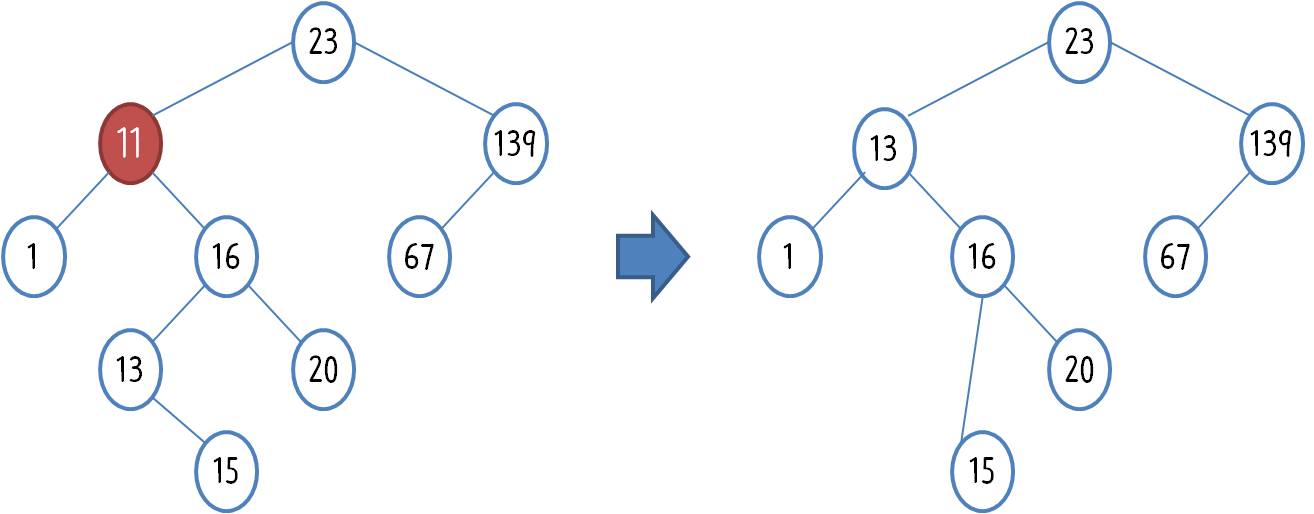

여기서 11 노드를 삭제 하려고 한다 그러면 오른쪽 트리의 왼쪽 자식 노드 (최소값) 을 옮겨 노드가 있던 자리에 놓고 오른쪽 자식노드를 부모 노드에 붙인다. (최소값 노드는 자식이 있더라도 오른쪽 자식 노드만 있음. )

레드 블랙 트리

이진 탐색트리가 기형적으로 성장해서 검색의 효율을 떨어뜨릴 수 있음. 순수 이진 탐색 트리의 경우 실제 데티터를 담는 경우 대체적으로 기형적으로 성장하기 때문에 검색 효율을 떨어 뜨린다.

이런 점에서 레드 블랙 트리는 이진 탐색트리를 균형있게 성장 하게 해준다. 레드 블랙 트리는 이름에서 알 수 있듯이 노드를 블랙 과 레드로 구분한다. 그래서 트리 노드에 레드 블랙 구분을 위한 필드가 필요하고, parent를 지정해 주어야 한다.
레드 트리가 균형을 유지 하기 위해서는 다섯가지 조건을 충족해야 한다.

1. 모든 노드는 빨간색과 검은색이다.
2. 루트 노드는 검은색이다.
3. 잎 노드는 검은색이다.
4. 빨간 노드의 자식들은 모드 검은색이지만 검은색 노드의 자식들이 모두 빨간 색일 필요는 없다.
5. 루트노드에서 모든 잎 노드 사이에 있는 검은색 노드의 수는 모두 동일하다.

레드 블랙 트리를 유지하기 위해서는 너무나~ 많은 규칙들이 필요하다. 이중 하나라도 만족하지 않는 다면 레드블랙트리가 아니게 된다.

BacktotheBasic - 탐색(순차탐색)

순차 탐색

순차 탐색은 처음부터 끝까지 모든 요소를 차례로 비교해서 데이터를 찾는 알고리즘이다. 한쪽으로만 탐색을 하기때문에 선형 탬색이라고 부른다. 비효율 적이지만 정렬되지 않은 데이터 집합속에서 데이터를 찾을 수 있는 유일한! 방법이고, 자료구조의 종류에 상관없이 모두 사용할 수 있고, 구현이 용이 하여 버그의 가능성이 낮기 때문에 높은 성능을 필요로 하지 않거나 데이터 집합의 크기가 작은 곳에서 자주 사용된다.

자기 구성 순차 탐색(self-organizing Sequential Search)

아무리 정렬되지 않은 데이터라도 차례로 찾는건 너무나 비효율 적이다.
100 개의 데이터가 있을 때 내가 찾는 데이터가 99 번째에 있으면 계속 해서 99번 비교를 해서 데이터를 가져와야 한다.
자기구성순차탐색은 ms의 최근 문서 목록과 같이 내가 자주 찾는 데이터를 앞으로 옮겨서 탐색을 용이하게 하는 방식이다.

자기구성법은 자주 사용되는 항목을 어떻게 구별하는가에 따라 아래와 같이 나눌 수 있다.

• 전진이동법
• 전위법
• 빈도계수법

전진이동법

전진이동법은 항목을 한번 탐색하고 나면 그 항목을 데이터 집합의 가장 앞에 위치하는 방법이다(MS 최근 문서).
하지만 특정 항목들이 집중적으로 탐색 대상이 되는것이 흔한일이 아니므로, 같은 또 다시 검색 될 가능성이 높은 데이터 집합에서 사용하는 것이 좋다.

전위법

전위법은 탐색된 항목을 바로 앞의 요소와 위치를 이동해서, 자주 탐색된 항목을 점진적으로 앞으로 옮긴다. 100개의 데이터 집합일때 n번째의 데이터는 n-1번의 선택을 받으면 가장 앞에 위치 할 수 있다. 이역시 비민주적일 수 있다. 왜냐하면 99번째 데이터는 98번의 선택을 받아야만 하고, 전위법의 경우 가장뒤에 있는 데이터가 가장많은 선택을 받더라도 데이터 집합의 크기가 크면 가장 앞에 올 수 있다는 보장을 받을 수 없다 (왜? )

계수법

요소들이 탐색된 횟수를 별도의 공간에 저장해 두고 탐색 된 횟수가 높은 순으로 데이터 집합을 재구성하는 전략의 알고리즘이다. 가장 민주적인 방법으로 보이지만 계수 결과를 저장하는 별도의 공간을 유지해야 하고 계수 결과에 따라 데이터 집합을 재배치 해야 하기때문에 비용이 많이 든다.

이진탐색

BacktotheBasic - 소팅(버블정렬/삽입정렬)

버블정렬

왜 버블정렬이라고 하는걸까? 알고리즘이 데이터를 저열하는 과정이 마치 물속에서 일어난 거품이 수면으로 올라오는 모습과 같다는 의미로 버블 정렬(BubbleSort) 라고 한다. 데이터가 순회를 하면서 이웃 요소끼리의 교환을 통해 정렬을 수행함.

CODE

package task.structure;
public class Sort {
 	public Sort() {

	}
	public static void main(String[] args) {
		int[] dataarr= {6,4,2,1,5,3};
		dataarr = BubbleSort(dataarr);

		for(int i = 0; i <dataarr.length ; i++){
			System.out.print(dataarr[i]);
		}
		System.out.println();
	}

	public static int[] BubbleSort(int[] arr){
		int cnt = 0;
		int len = arr.length;
		for(int i = 0; i <len ; i++){
			for(int j=0; j < len - (i+1); j++){
				cnt +=1;
				if(arr[j] > arr[j+1]){
					int temp = arr[j+1];
					arr[j+1] = arr[j];
					arr[j]= temp;
				}
			}
		}
		System.out.println(cnt);
		return arr;
	}
}

1. 6 > 4 ? change : stay –> [4

   6

   2

   1

   5

   3]

2. 6 > 2 ? change : stay –> [4

   2

   6

   1

   5

   3]

3. 6 > 1 ? change : stay –> [4

   2

   1

   6

   5

   3]

4. 6 > 3 ? change : stay –> [4

   2

   1

   5

   6

   3]

5. 6 > 3 ? change : stay –> [4

   2

   1

   5

   3

   6]

6. 4 > 2 ? change : stay –> [2

   4

   1

   5

   3

   6]

7. 4 > 1 ? change : stay –> [2

   1

   4

   5

   3

   6]

8. 4 > 5 ? change : stay –> [2

   1

   4

   5

   3

   6]

9. 5 > 3 ? change : stay –> [2

   1

   4

   3

   5

   6]

10. 5 > 6 ? change : stay –> [2|1|4|3|5|6] . . n개를 정렬해야 한다면 이렇게 n(n-1)/2 번의 비교를 해야 함.

만약에 {2,1.3,4,5,6 } 이런 배열을 sorting한다면 ?

[213456]
[123456]
[123456]
[123456]
[123456]
[123456]
[123456]
[123456]
[123456]
[123456]
[123456]
[123456]
[123456]
[123456]
[123456]
[123456]

2와 1을 바꾼 후에 더 이상 정렬을 할필요가 없는데도 루프를 돌면서 비교를 수행한다. 정렬이 되어 있는경우 루프를 취소하고 빠져나오도록 하기 위해서는 어떻게 해야 할까?

플래그를 한번 달아봤다. 순환 중 change가 되지 않으면 더이상 정렬하지 않아도 되는것으로 판단하도록 했다.

CODE

public static int[] BubbleSort(int[] arr){
		int cnt = 0;
		int len = arr.length;
		boolean flag= true;
		for(int i = 0; i <len ; i++){
			if(flag){
				flag = false;
				for(int j=0; j < len - (i+1); j++){
					cnt +=1;
					if(arr[j] > arr[j+1]){
						flag = true;
						int temp = arr[j+1];
						arr[j+1] = arr[j];
						arr[j]= temp;
						System.out.println("change" + arr[j+1] + "<->" +temp);
					}

					System.out.println( arr[j] + " / "+ arr[j+1] + "-->"+ printArray(arr));

				}
			}

		}
		System.out.println(cnt);
		return arr;
	}

change7<->2
2 / 7-->[2713456]
change7<->1
1 / 7-->[2173456]
change7<->3
3 / 7-->[2137456]
change7<->4
4 / 7-->[2134756]
change7<->5
5 / 7-->[2134576]
change7<->6
6 / 7-->[2134567]
change2<->1
1 / 2-->[1234567]
2 / 3-->[1234567]
3 / 4-->[1234567]
4 / 5-->[1234567]
1 / 2-->[1234567]
2 / 3-->[1234567]
3 / 4-->[1234567]
4 / 5-->[1234567]
15
[1234567]

삽입 정렬

설명… CODE

전체 코드

CODE

 package task.structure;


public class Sort {

	int[] array = new int[20];


 	public int[] getArray() {
		return array;
	}

	public void setArray(int[] array) {
		this.array = array;
	}

	public Sort() {

	}

	public static void main(String[] args) {
		int[] dataarr= {5,1,6,4,2,3};
		Sort sort = new Sort();
		sort.setArray(dataarr);
		System.out.println(printArray(sort.getArray()));
		//System.out.println(printArray( sort.bubbleSort()));
		//System.out.println(printArray( sort.insertionSort()));
		System.out.println(printArray( sort.quickSort()));
	}

	public static String printArray(int[] arr){
		String result = "[" ;
		for(int i = 0; i <arr.length ; i++){
			result += arr[i];
		}
		result += "]";
		return result;
	}

	private int[] bubbleSort(){
		int[] arr = getArray();
		int cnt = 0;
		int len = arr.length;
		boolean flag= true;
		for(int i = 0; i <len ; i++){
			if(flag){
				flag = false;
				for(int j=0; j < len - (i+1); j++){
					cnt +=1;
					if(arr[j] > arr[j+1]){
						flag = true;
						int temp = arr[j+1];
						arr[j+1] = arr[j];
						arr[j]= temp;
						System.out.println("change" + arr[j+1] + "<->" +temp);
					}

					System.out.println( arr[j] + " / "+ arr[j+1] + "-->"+ printArray(arr));

				}
			}

		}
		System.out.println(cnt);
		return arr;
	}

	private int[] insertionSort(){
		System.out.println("start InsertionSort! ");
		int[] arr = getArray();
		int cnt = 0;
		int len = arr.length;
		for(int i = 1; i < len ; i++){
			if(arr[i-1] > arr[i]){//오른쪽이 더 작으면
				int num = arr[i];
				int j = 0;
				while(num > arr[j]){
					j++; //1
				}
				//System.out.println( num + "have to insert to" + j );
				arr = change(i, j, arr);
			}

		}

		return arr;
	}

	private int[] change(int oldi, int newi, int[] arr){
		int temp = arr[oldi];
		for(int i = oldi; i > newi; i--){
			arr[i] = arr[i-1];
		}
		arr[newi] = temp;
		return arr;
	}

	private int[] quickSort(){
		int[] arr = getArray();
		System.out.println(arr.length);
		quickSort( 0, arr.length-1);
		return getArray();
	}

	private void swap(int ai, int bi){
		int[] arr = getArray();
		int temp = arr[bi];
		arr[bi] = arr[ai];
		arr[ai] = temp;
	}

	private int partition(int left, int right){
		System.out.println("partition::: " + left +"/" + right);
		int[] arr = getArray();
		int first = left;
		int pivot = arr[first];

		while(left <= right){
			while(arr[right] > pivot && left < right){
				--right;
			}
			while(arr[left] <= pivot && left < right){
				++left;
			}


			System.out.println("left:" + left + " right:" +  right);
			if(left < right ){
				swap(left, right);
				System.out.println(printArray(arr));
			}else{
				break;
			}
		}

		swap(first, right);
		System.out.println(printArray(arr));

		System.out.println("retrun::" + right);
		return right;
	}

	private void quickSort(int left, int right){

		if(left < right ){
			int index = partition( left, right);

			quickSort( left, index-1);
			quickSort( index+1, right);
		}
	}
}