이진 탐색

이진 탐색은 정렬된 데이터 집함에서 사용할 수 있는 ‘고속’ 탐색 알고리즘이다.

1. 데이터 집합의 중앙에 있는 요소를 고른다.
2. 중앙 요소의 값과 찾고자 하는 값을 비교 한다.
3. 목표한 값이 중앙요소보다 적으면 왼편에 대해 검색하고, 크면 오른쪽으로 이진 탐색을 수행한다.
4. 찾고자 하는 값을 찾을때 까지 1~3번을 수행한다.

이진 탐색의 성능

이진 탐색은 탐색을 시도할 때 탐색 대상의 범위가 1/2 로 줄어든다. 데이터집합의 크기를 n이라고 하고 탐색 횟수를 x라고 할때

탐색횟수는 X= log_2*n이 된다.

이진탐색트리

이진 탐색트리는 말그대로 이진 탐색을 위한 이진 트리이다.

왜 이진 탐색 트리가 필요한 걸까?. 이진 탐색을 하기위해서는 첫째, 데이터의 처음과 끝을 알아야 하고, 둘때, 순식간에 데이터 집합의 중앙요소를 계산하고 접근 가능해야 한다. 배열의 경우 인덱스를 이용해서 중앙에 있는 요소를 쉽게 계산 및 접근이 가능하지만 데이터 집합이 리스트라고 생각해 보면, head 와 tail을 이용해서 처음과 끝을 알 수 있지만 그 중앙요소를 알수없기 때문에 이진탐색을 위해서는 이진 탐색 트리 구조가 필요하다.

이진 탐색트리의 규칙은 간단하다.

왼쪽 자식 노드는 부모노드보다 작고 오른쪽 자식노드는 부모 노드 보다 커야 한다.
탐색 또한 간단하다.

목표 값이 현재 노드 보다 더 큰경우 오른쪽 하위 트리에 대해서 다시 한번 탐색을 한다.
반대로 더 작은 경우 왼쪽 하위 트리에 대해서 다시 한번 탐색한다.
이렇게 탐색을 반복한다.

삽입은 조금 복잡하다. 우선 새 노드가 삽입 될 곳을 찾아야 한다. 이진 탐색을 통해서 새 노드가 놓일 곳을 찾아내야 한다.

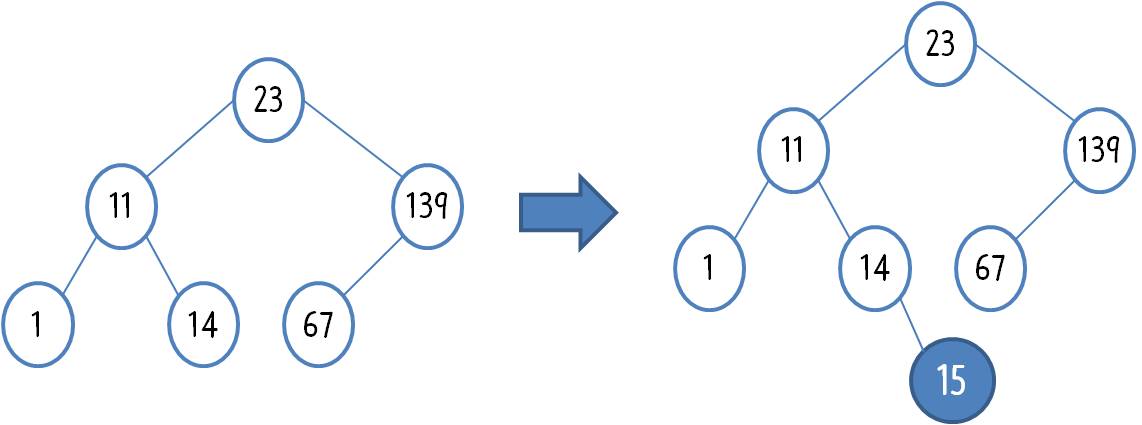
이렇게 생긴 트리데 15를 넣는다면 아래와 같이 진행 될 것이다.
23부터 비교를 한다. 23 보다 15가 더 작다. 23 의 왼쪽 자식 노드가 비어있는지 확인한다. 비어있지 않으므로 왼쪽 트리를 다시 탐색 한다. 11과 15를 비교한다. 11 보다 15가 더 크다. 11의 오른쪽 자식 노드가 비어있는지 확인한다. 비어 있지 않아서 다시 오른쪽 트리를 탐색 한다.
14와 15를 비교한다. 14 보다 15가 더 크다. 14의 오른쪽 자식 노드가 비어있는지 확인하다. 비어있다!! 14의 오른쪽 노드로 15를 넣는다.

이진 탐색 노드의 삭제는 어떻게 될까?
조금 더 복잡한 이진 탐색 트리를 예로 들어 보자

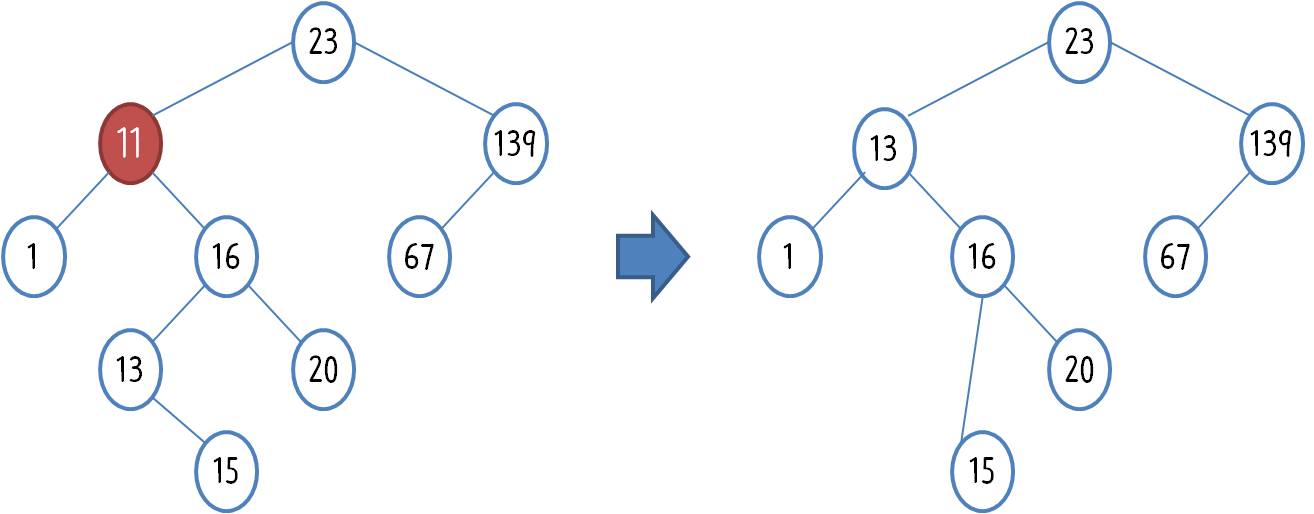여기서 11 노드를 삭제 하려고 한다 그러면 오른쪽 트리의 왼쪽 자식 노드 (최소값) 을 옮겨 노드가 있던 자리에 놓고 오른쪽 자식노드를 부모 노드에 붙인다. (최소값 노드는 자식이 있더라도 오른쪽 자식 노드만 있음. )

레드 블랙 트리

이진 탐색트리가 기형적으로 성장해서 검색의 효율을 떨어뜨릴 수 있음. 순수 이진 탐색 트리의 경우 실제 데티터를 담는 경우 대체적으로 기형적으로 성장하기 때문에 검색 효율을 떨어 뜨린다.

이런 점에서 레드 블랙 트리는 이진 탐색트리를 균형있게 성장 하게 해준다. 레드 블랙 트리는 이름에서 알 수 있듯이 노드를 블랙 과 레드로 구분한다. 그래서 트리 노드에 레드 블랙 구분을 위한 필드가 필요하고, parent를 지정해 주어야 한다.
레드 트리가 균형을 유지 하기 위해서는 다섯가지 조건을 충족해야 한다.

1. 모든 노드는 빨간색과 검은색이다.
2. 루트 노드는 검은색이다.
3. 잎 노드는 검은색이다.
4. 빨간 노드의 자식들은 모드 검은색이지만 검은색 노드의 자식들이 모두 빨간 색일 필요는 없다.
5. 루트노드에서 모든 잎 노드 사이에 있는 검은색 노드의 수는 모두 동일하다.

레드 블랙 트리를 유지하기 위해서는 너무나~ 많은 규칙들이 필요하다. 이중 하나라도 만족하지 않는 다면 레드블랙트리가 아니게 된다.